В.В.Смирнов. Авторское предисловие
Как делать летающие тарелки
Предлагаем минимум по программе «Новые алгебраические числа».
1) В первом фрагменте мы покажем, что общий случай математики является нерациональным
(На сегодняшний день пока что!). А поскольку математика – царица всех наук, то и физика,
и само Мироздание в общем случае нерациональны. А под знаком нерациональности –
неопределенности скрываться может любой объект, в том числе и Господь Бог.
Уже давно в умах человеков витает мысль, что Наука и Религия должны объединиться
и составить единое целое. В том, собственно, никто не возражал, не было связующего звена.
Теория V-функций, как раз и является связующим звеном.
И тут вспоминается программа американских метафизиков, обнародованная лет 50 назад.
По ней люди в начале 21 века должны найти Бога и установить с ним связь. Мы, конечно,
Бога не нашли, но дорогу в математику Ему открыли.
2) Что такое функция V? На ней построена физико-математическая модель летающей тарелки,
эксперимент Филадельфия и пр. Если мы, конечно, не ошиблись,
то при правильном развороте событий, лет через пять – десять
можно ставить строительство летающих тарелок на конвейер.
Любой стране мира под гарантийное письмо в три миллиарда долларов мы согласны
передать расчетный материал. Оплата по факту.
Валерий Смирнов. Новые алгебраические числа
Предисловие
1. Этот фрагмент является первым, представляющим новую алгебраическую теорию –
теорию V функций.
2. У этих чисел есть своя история. Одним из упомянутых, кто усомнился
в достаточности двух чисел, был Лейбниц (17в.). Он полагал, что
операция извлечения корня из числа Z=a+bi порождает новые категории
мнимых. (Хрестоматия по истории математики. Москва: издательство "Просвещение", 1976 г.,
стр.88). Позднее было объявлено, что Лейбниц допустил «случайный недосмотр»,
однако прав был :
Z1/n (=)Q(v) R1/n(cosj/n+isinj/n)(cos2π/n+fsin2π/n) ≡ v6
Новая категория мнимых, то же можно и с действительным числом.
3. Следующим был Гаусс. Предметом его докторской диссертации было
основное уравнение алгебры (1799г. стр.95, там же) Он высказал
мысль о том, что полином P(х) можно разбить на ряда классифицированных
подмножеств и каждое такое должно разрешаться при помощи особых
алгебраических чисел изоморфных и даже не изоморфных.
Я назвал эту мысль моделью Гаусса :
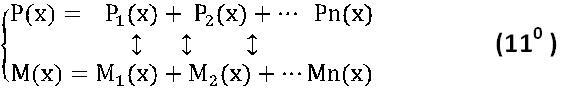
4. В 19 веке два немецких математика К. Вейерштрасс и Ф. Фробениус
продолжили тему и установили, что любая числовая система над
полем действительных чисел, в которой законы операций те же,
что и для рациональных чисел, совпадает с полем действительных,
либо с полем чисел Z ( там же, стр.93). Знака совпадения в алгебре
нет, поэтому придумано условное равенство, введена орфография –
символ поля. Из краткого толкования теоремы «с одной стороны…
с другой стороны…» следует, что объект изложен дуально. Особо это
очевидно, если пустить в ход разложение в линейные множители :
П(х)=(x-x1)(x-x2)…(x-x5) (=) Q(v)(x1+v)5 =(x2+v)5=…=(x5+v)5
Из разложения в Q(v) по теореме В-Ф следует :
[(x1+v)5 ]1/5 = [(x2+v)5 ]1/5 → x1+v = x2+ v (!)
(!) Сократить тут подобные члены нельзя – абсурд : х1 ≠ х2. Остается
одно : 
неопределенность = неопределенности. И окончательно :
f (=) Q(x) 1 = ∾ (130 )
fi (=) Q(i) i = i∾ (140)
Числа дуальные алгебраические нерациональные, никакого векторно-
числового измерения.
5. Из св. 90 следует, что любой кв. трехчлен имеет не менее шести корней-
- два из множества Z и четыре из множества V чисел. Каждый может их
найти, руководствуясь примером 5.
6. Единственным надполем на сегодняшний день следует считать поле
чисел v6 - [Q(v6 )]. Все остальные подполями : g(x), g(z) и т. д. (150 )
======
А теперь непосредственно фрагмент I:
I
1) Дано числовое поле F , не эквивалентное действительному x:
Q(F)≠ Q(x) и дано число f в нем
Q(F) Q(x)
f1+4k (=) 1 k=0, 1, 2, 3 . . .
f2+4k = -1 ( 10 )
f3+4k (=) -1
f4+4k = 1
Я назвал это число фантомом от англ. призрак (число-невидимка)
Знак (=) условным равенством, что означает в данном случае, что
в ход пошли нерациональные математические построения и орфо-
графия, которая определяет поле (подполе). Само собой, возникает
понятие нового поля комплексных чисел F - x
2) При тех же условиях, что и выше, числовое поле Fi , не эквивалентное
полю чисел z: Q(Fi)≠Q(z) и число fi
Q(Fi) Q(z)
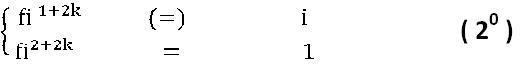
Поле комплексных чисел Q(Fi – z)
3) Появляются новые комплексные числа, я назвал их V- числами. Их десять:
v1 = a +cf v2=a +dfi
v3 = a +cf+dfi v4=a +bi + cf
v5 =a + bi +dfi v6 =a + bi + cf + dfi
v7 = bi + cf +dfi v8 = bi + cf
v9 = bi +dfi v10 = cf + dfi
Количество тут рассчитывается по формуле 2n -1, где n- кол.
элементарных чисел. Эта формула верна для всех известных случаев
Итак, чисел элементарных четыре, плюс комплекс z, плюс десять
комплексов v- итого пятнадцать. Очевидно, что комплекс z является
частным случаем комплексного числа . Отсюда просходит разделение:
на ортодоксальную теорию z- функций и новую теорию v- функций.
Ясно, что имеется тождественность функций по модулю и аргументу.
Отсюда возникают понятия о тождественных преобразованиях и
первые аксиомы поля:
f ∙ 0 = 0 ( 30 ) fi ∙ 0 = 0 ( 40 )
Допускаются все шесть действий алгебры, а также коммутативные,
ассоциативные и дистрибутивный законы.
II
Полезность
Мы посмотрим полином P(x) -основное уравнение алгебры, а именно
подмножество П(x) = 0, т.е. такое, в котором обязательно фигурирует
фантом.
Пример 1
Дано ур-ние по основанию v1:
Q(F-x)
(x+f)=x5+5x4f+10x3f2+10x2f3+5xf4+f5 = . x5+5x4f-10x3-10x2 f+5x+f (=)
Q(x) (=) x5+5x4-10x3-10x2+5x+1=0
Корни алгебраические:
Данное можно определить как ур-ние с треугольником Паскаля от
основания (x+1)5 , а знакообразование от основания (x+i)5 ( 50 )
От этих рассуждений переходим к тождественным построениям.
В самом деле
x5-10x3+5x=R5 cos5j ; 5x4-10x2+1=R5 sin5j
и, таким образом (x+f)5 (=)Q(x) R5 (cos5j+sin5j). В нашем случае
R5 (cos5j + sin5j) = 0 , откуда cos5j = -sin5j и далее
xk = ctg [1350 +π (k-1)]/n и угловая мера корней:
x1-5 = 270, 630, 990, 1350, 1710
Я назвал этот и ему подобные возвратно-фантомными с треугольником
Паскаля равным нулю: П(х) = 0. Приводится формула общего случая
для v1 : (ax + cf)n = Q(x) П(х) = 0
xk = c/a ctg[1350 +π(k-1)]/n (1.1)
Здесь можно положить окружность единичного радиуса,как график
функции. Тогда каждый корень выразится своей угловой мерой через
радиус-вектор, причем будет работать формула jk=j1+Δ(k-1) ( 60 )
т.е. каждый последующий угол равен предыдущему плюс некоторое
Δ = const. Такую конструкцию имел и Муавр в своем ур-нии xn-1=0
Я назвал такую симметричной радиус-векторной решеткой. Отметим,
что все корни уравнения действительны.
Пример 2
Дано ур-ние по основанию v2 :
(х+fi)5 = x5+5x4 fi+10x3 (fi)2+10x2 (fi)3+5x (fi)4+(fi)5 (=)
(=) Q(Fi-z) x5+5x4 i+10x3+10x2 i+5x+I = 0
Корни алгебраические:
Данное определим,как ур-ние с треугольником Паскаля по основанию
(x+i)5 , а знакообразование от основания (x+1)5 ( 70 )
Положим i=c, тогда придем к ур-нию (x+cf)5 откуда
хk = i ctg[1350+π(k-1)]/n и общий случай (ах+dfi)n (=) Q(z) … 0
xk = di/a ctg [1350+π(k-1)]/n (1.2)
Корни: x1-5 = i ctg270 и т. д.
Заметим, что и здесь симметричная радиус-векторная решетка, но
все корни мнимы.Анализ формул (1.1-1.2) по пределу
lim jk=(1-n) = [1350+π(k-1)]/n = (0 ÷ π) ( 80 )
позволяет заключить, что решетка расположена в двух четвертях
окружности единичного радиуса.
Пример 3
Дано ур-ние по основанию v4 :
(x+i+f)5 =[(x+i)+f]5 (=)Q(z) x5+5x4 (i+1)-20x3 (i-1)-40x2 (i-1)-40x (i-1)+16(i+1) = 0
Корни алгебраические:
Как видно, треугольника Паскаля тут уже нет. Примем x+i = y,
тогда данное приводится к виду (y+f)5 (=) Q(z)… 0. И корни :
x1-5 = ctg 270 – i и т. д.
Пример 4
Дано ур-ние по основанию v5 :
(x+i+fi)5 (=) Q(z) x5 +10x4 I -20x3 -20x -8i = 0
Корни алгебраические :
Покажем для начала как оно вычислено
(x+i+fi)5 = [(x+i)+fi]5 (=)Q(z)(x+i)5 + 5i(x+i)4 + 10(x+i)3 + 10i(x+i)2 + 5(x+i) +i =…
Примем x+i = y , тогда (y+fi)5 и т. д.
Корни x1-5 = i ctg 270 – i = i ctg (270 -1) и т. д.
Приводим примерные измерения корней и радиус-векторную решетку:
х1 ≈0,9626i ≈ ctg 46,0910
х2 ≈-0,4904i ≈ 116,127 0 Δ2-1≈70,0360
х3 ≈ -1,1584i ≈ 139,1050 Δ3-2≈23,070
х4 =-2i ≈ 153,4350 Δ4-3≈14,240
х5 ≈-7,3137i ≈ 172,2140 Δ5-4≈18,780
Решетка тут является несимметричной.
Пример 5
В предыдущих примерах была дана функция v , потому и были вычи-
слены корни. Тут обратная задача - по коэффициентам данного
вычислить корни алгебраические.
Дано П(x) = 0.
x5 +5x4 (4+6i) – 60x3 + 10x2 (196-76i) +5x(636+800i) – 2096 – 2104i = 0
Корни алгебраические :
1) Треугольник Паскаля (x+v6)5 (=) П(х). Всегда пускаем в ход
функцию v6 и св. 10, 20.
2) Измерение С2/ :
5x4 v6 (=)Q(x) 5x4 (z1+z2) = 5x4 (4+6i) → z1+z2 = 4+ 6i
3) Измерение С3/ :
v62 =(z1+z2) – 2z22 = 16+48i – 36 -2z22 = - 6 → z22 = -7 + 24i =
= 25( cos106,260 + i sin106,260 ) →z2-1,2=5(cos53,130 + i sin53,130 ) =
±(3+4i)
z1-1,2= 4 + 6i – z2-1,2 = 4 +6i ± (3+4i) = 1+2i ; 7+10i
Из последнего четыре версии функции v:
V1=z1-1+z2-1= 1+2i+3+4i=4+6i V2=z1-1+z2-2=1+2i-3-4i ≠ 4+6i
V3=z1-2+z2-2=7+10i-3-4i=4+6i V4=z1-2+z2-1=7+!0i+3+4i ≠ 4+6i
Укажем сразу истинную версию функции v0 = 1+2i+3f+4dfi.
Поскольку функции V1 , V3 сопряжены с С2/, С3/ ,
постольку истинную функцию v0 можно установить
только при измерении С4/ ( 90 )
Корни:
Подстановка x+1+2i = y 3+4i = z т.е. (y+fz)5 (=) 0 →
→ y1=zctg270= (3+4i)ctg270 →
X1 = (3+4i) ctg 270 – 1 – 2i ≈ 4,8878+5,8504i
X2 = (3+4i) ctg 630 - 1 - 2i ≈ 0,5285+0,0381i
X3 =(3 +4i) ctg 990 – 1 – 2i ≈ -1,4751-2,6395i
X4 = (3+4i) ctg 1350 – 1 – 2i = -4-6i
X5 = (3+4i) ctg 1710 – 1 – 2i ≈ -19,9412-27,255i
Лемма
Пусть дан полином П(x) = 0 степени n. Если x+v = x+a+bi+cf+dfi, то
xkQ(z) = (c+di) ctg [ π(k-0,25)]/n – a – bi ( 100 )
Анализ леммы показывает, что все четыре числа являются алгебраи-
ческими , необходимыми и незаменимыми. Из последнего второе
кол. корней :
x6 = x1 + v0 =(3+4i)ctg270-1-2i + 1+2i +3f + 4fi = (3+4i) (ctg270 +f)
. . . . . . . .
x10 = x5 + v0 = (3+4i) (ctg1710 + f)
=======
Материал предоставлен автором и
размещен на сайте Nauki-Online.ru
22 июня 2013 года
Валерий Смирнов. Основная теорема алгебры
Второй фрагмент |III
Пример 6
(х+f1/√2)3 (=) g(z) 0, где корни
х1 = 1/√2ctg450 =1/√2
х2 = 1/√2ctg1050 = (-2+√3)/√2
х3 = 1/ √2ctg1650 = (-2-√3 )/√2
Откуда
R1=(x1 2 + c2 )0,5 = (0,5+0,5)0,5 = 1
R2=(x2 2 + c2 )0,5 =[(7-4√3)/2 + 0,5]0,5 ≈ 0,732
R3=(x3 2 + c2 )0,5 =[(7+4√3)/2 + 0,5]0,5≈ 2,732
Из последнего основная характеристика П(x) : R1-n ≠0 (160 )
Мы посмотрим теперь полином П(a) : a2 + b2 = 1, где r(1-n) = 1 (170 )
Очевидно, a=cosj b=sinj.
Покажем тождественную связь между полиномами большим и малым
( см. пример 1):
x5+5x4 -10x3 – 10x2 + 5x +1 =a5 /b5 + 5a4 / b4 - … + 1 =
= (a5 + 5a4 b – 10a3 b2 – 10a2 b3 + 5ab4 + b5 )/b5 (=) g(v1 ) [(a+fb)/b]5=
= ( x+f )5 = R5 ( cos5j + fsin5j )
И, таким образом, приходим к формуле : R(1-n) = 1/b(1-n) =1/sinj(1-n) (180 )
Пример 7
cos2j + cosj = 2cos1,5jcos0,5j= 0
Арифметика. (Здесь и далее идут в ход Пифагоровы построения – тройки
чисел)
a2 – b2 + a = 2a2 + a -1 = 0 a1,2 = 0,5; -1
Очевидно, речь идет о точке М(0,±1) окружности единичного радиуса.
И тут возникает вопрос: сколько корней положить на каждую функцию.
Я установил далее минимум и максимум функции для полунечетных
аргументов (n/2
одним меньше. (190 )
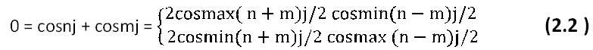
откуда
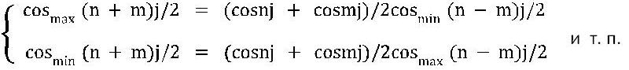
Для случая 0,5j
0 = cosnj + cosmj = 2 cosmin(n+m)j/2cos0,5j = cosmax(n+m)j /2 (2.3 )
и, вернувшись к задаче
cosmax 1,5j : j1,2 = [ 900 +π (k-1)]/1,5 = 600 ; 1800
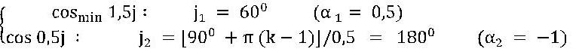
Таким образом 0 = cosmin 1,5j cos 0,5j = cosmax 1,5j
Пример 8
cos5j+cos2j = 2cos3,5jcos1,5j = 0 M(0;±1)
Максимальная и минимальная функция.
1) Арифметика:
a2 -10a3 b2 + 5a b4 + a2 – b2 = 16a5 – 20a3 + 2a2 + 5a -1 = 0
2) Геометрия:
|
|
cоsmin 3,5j = cos : 1800/7 , 5400/7 , 9000/7 |
|
cosmax 1,5j = cos : 600 , 1800 |
|
|
cosmax 3,5j = cos : 1800/7 , 5400/7 , 9000/7 , |
|
cosmin 1,5j = cos : 600 |
Тут следует упомянуть радиус-векторную решетку. Я назвал такую частично
симметричной.
3) Функции
0 = cosmin 3,5j =( 16a5 – 20a3 + 2a2 + 5a-1) / (2a2 + a -1)= 8a3 -4a2 -4a +1
0 = cosmax 3,5j =( 16a5 -20a3 + 2a2 +5a – 1) / (2a -1) = 8a4 +4a3 – 8a2 -3a +1
Заключаю, что кроме степени ( n ) есть еще порядок ( р ) уравнения. Под
степенью n я понимаю аргумент эквивалентной тригонометрической
функции, под порядком p старшая степень ур-ния. (190 )
Таким образом, уравнение четвертого порядка степени 3,5(max), третьего
порядка степени 3,5(min)…
Пример 9
cosmax 3,5j + cosmin 3,5j = 8a4 + 12a3 – 12a2 – 7a +2 = 0 (cм. предыд. пример)
Радиус-векторная решетка:
cosmax 3,5j + cosmin 3,5j = cosmin 3,5j(a+1) + cosmin 3,5j = cosmin 3,5j(a+2) = 0
Корни:
1) cosmin 3,5j = 0 → j1-3 : 1800/7 ; 5400/7 ; 9000/7
2) a ≡ x = 2 (!)
(!) Частично симметричная р-в решетка с вырождением функции.
IV
Деление полиномов нацело
Пример 10
1) (x+f)10 /(x+f)2 (=) g(z) П(х)1 / П(Х)2 =
= (x10+10x9 – 45x8 -120x7 +210x6 +252x5 – 210x4 – 120x3 +45x2 +10x -1) /
/(x2 + 2x-1)=x8 + 8x7 -60x6 +8x5 +134x4 -8x3 -60x2 -8x +1
Операция задумана тут в поле чисел v, но проведена в z – числах
2) Корни :
J1-8 = 13,50 ; 31,50 ; 49,50 . . . 85,50 ; 103,50 ; 121,50 ; 139,50 . . . 175,50
Необходимое условие : р-в решетка одного содержится в р-в решетке
другого. (200 )
И в результате П(х)1 / П(х)2 = Т(р). Назовем полином Т(р) трековым.
Укажем здесь принцип делимости нацело для целых n и k
n1 /n2 = 5k (210 )
т.е. полученый Т(p) можно назвать уравнением восьмого порядка
десятой, пятидесятой, двести пятидесятой и т. д. степени. Сам Т(p)
имеет только каноническое разложение в линейные множители :
Т(p) = (х-х1 )(х-х2 ) . . . (х-хр ) где р – порядок (220 )
Очевидно, Т(р) производное от П(х).
VОсновное уравнение алгебры
Покажем тут несколько своих предложений.1) Предложение о степени полинома Р(х)
Фактически тут порядок р принимался за степень n. Де-факто порядок р
есть сумма-разность степеней, в примере 10, например, р= n1-n2=10-2=8
На самом деле нам известны всего два ур-ния, где р=n. Это (x+z)n = 0 и
(x+v)n =g(z)…0. Во всех остальных р≠n (230 )
2) Предложение о составе алгебры
«Алгебра есть арифметика шести действий плюс эквивалентная геометрия» (240 )
Св. 240 является обязательным. Из необязательности происходят
теоретические ошибки. Из «мемуара об условиях разрешимости
уравнения в радикалах» 1846г (там же, стр. 102-106) видно, что Галуа
отработал проблему арифметически, которую засчитали за алгебру.
Дело в том, что в состав алгебры всегда входила геометрия и истинно
алгебраической нужно считать систему ур-ний, где арифметика дублирует
геометрию и наоборот. Это потому, что арифметика и геометрия лишь
тождественные дисциплины и по одной и той же проблеме могут
разойтись в разные стороны.
3) Из последнего происходит основная теорема алгебры (ОТА).
Пусть дан полином P(x) общего вида (Галуа). Очевидно, он имеет свою
р-в решетку, которую через ctgj можно разместить в 1-й и 2-й четверти
окр. ед. радиуса. Допускается, что всегда найдется полином П(х) с такой
густой решеткой, что она совместится с первой. Это, как раз, тот случай,
когда арифметика расходится с геометрией. На языке алгебры
P(x)∙t(p)=П(х) где t(p) тоже какое-то порядковое ур-ние (250 )
Для полиномов П(х) мы такую возможность показали, но не было случая,
чтобы то же для Р(х).
Что будет, если св. 250 будет доказано… Самое главное – будет закрыто
множество F Гаусса и мы точно будем знать предельную полноту
алгебраической функции. Как известно, числа формируют функции в т. ч.
и прикладные, а те, в свою очередь, либо «тянут либо не тянут» материал.
Все зависит от достаточной полноты функции. Тут можно припомнить Эйнштейна.
В 20х годах прошлого века он взялся за «Единую теорию поля». Теорию он
так и не написал, позднее жаловался, дескать, слабовато знает математику,
вот если бы получше, тогда что-то и срослось бы. События дальние показали,
что знал он математику вполне прилично, ибо на его место пришли сотни
светлейших голов – математиков, но теорию так и не написали.
И тут возникает вопрос: а те ли функции пускались в ход.
В примере 5 показано превосходство функции V, Эйнштейн эту функцию не знал.
4) Следует отказаться от ортодоксального толкования ОТА – «хотя бы один
корень в комплексной области» Дело в том, что предложение Гаусса
мы считаем главным предложением алгебры, а в его предложении допускается
«значение…которое не содержится ни в каком виде» т.е. даже не в числах Z.
Вместо этого св. 250, как «Основная теорема алгебры» с необходимым требованием
– закрыть множество F Гаусса.
=======
Материал предоставлен автором и
размещен на сайте Nauki-Online.ru
24 июня 2013 года
